|
ICE and ICEBERGS |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
HOME SITE INDEX CATAMARAN HULL SOLAR PANELS ELECTRIC MOTORS BATTERIES CREW EXPEDITION SPONSORS |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Physical Properties of Ice
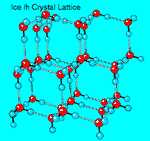
Crystalline
Structure of Ice. Ice can assume a
large number of different crystalline structures, more than any
other known material. At ordinary pressures the stable
phase of ice is called ice I, and the various high-pressure
phases of ice number up to ice XIV so far. (Ice IX
received some degree of notoriety from Kurt Vonnegut's novel Cat's
Cradle.)
There are two closely related variants of ice I: hexagonal ice Ih, which has hexagonal symmetry, and cubic ice Ic, which has a crystal structure similar to diamond. Ice Ih is the normal form of ice; ice Ic is formed by depositing vapor at very low temperatures (below 140°K). Amorphous ice can be made by depositing water vapor onto a substrate at still lower temperatures.
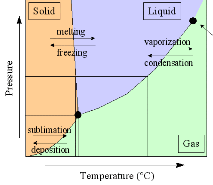
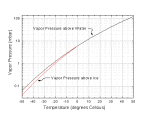
Phase Diagram of Water and Ice. The plot at right shows the phase diagram of water (click on the image for an expanded version). The triple point of water -- when ice, water, and water vapor can coexist -- is at a temperature of 0.01C (0C = 273.16K), and a pressure of 6.1 mbar. Water is the only substance which we commonly experience near its triple point in everyday life.
Pwater(T) = [2.8262e9 - 1.0897e6*T - 94934*T2 + 582.2*T3]exp(-5450/TK) Pice(T) = [3.6646e10 - 1.3086e6*T - 33793*T2]exp(-6150/TK)
where pressures P are in mbar, the temperature T is in degrees Celsius, and TK is in degrees Kelvin (Note 0C = 273.16K).
These approximate expressions are accurate to better than 0.1 percent from -50C to 50C.
All the solid phases of ice involve the water molecules being hydrogen bonded to four neighboring water molecules. In all cases the two hydrogen atoms are equivalent, with the water molecules retaining their symmetry, and they all obey the 'ice' rules: two hydrogen atoms near each oxygen, one hydrogen atom on each O····O bond.j The H-O-H angle in the ice phases is expected to be a little less than the tetrahedral angle (109.47°), at about 107°.
Both the critical points are shown as red circles in the phase diagram, above. Beyond the critical point in the liquid-vapor space (towards the top right, above), water is supercritical existing as small but liquid-like hydrogen-bonded clusters dispersed within a gas-like phase [456], where physical properties, such as gas-like or liquid-like behavior, vary in response to changing density. The properties of supercritical water are very different from ambient water. For example, supercritical water is a very poor solvent for electrolytes, but excellent for non-polar molecules, due to its low dielectric constant and poor hydrogen bonding. The physical properties of water close to the critical point (near-critical) are particularly strongly affected [677].
The critical point and the orange line in the ice-one phase space refer to the low-density (LDA) and high-density (HDA) forms of amorphous water (ice) [16]. Although generally accepted and supported by some experimental evidence [754], the existence of this second, if metastable, critical point is impossible to prove at the present time and is disputed by some [200, 618, 628].
The transition between LDA and HDA is due to the increased entropy and van der Waals contacts in HDA compensating for the reduced strength of its hydrogen bonding. The high-pressure phase lines of ice-ten (X) and ice-eleven (XI) [81] are still subject to experimental verification. Two different forms of ice-eleven have been described by different research groups: the high-pressure form (also known as ice-thirteen) involves hydrogen atoms equally-spaced between the oxygen atoms [84] (like ice-ten) whereas the lower pressure low temperature form utilizes the incorporation of hydroxide defect doping (and interstitial K+ ions) to order the hydrogen bonding of ice Ih [207], that otherwise occurs too slowly. Another ice-ten has been described, being the proton ordered form of ice-six (VI) occurring below about 110 K. Only hexagonal ice-one (Ih), ice-three (III), ice-five (V), ice-six (VI) and ice-seven (VII) can be in equilibrium with liquid water, whereas all the others ices, including ice-two (II, [273]), are not stable in its presence under any conditions of temperature and pressure.
The low-temperature ices, ice-two, ice-eight (VIII), ice-nine (IX) and ice-eleven (low pressure form) all possess (ice-nine incompletely) low entropy ordered hydrogen-bonding whereas in the other ices (except ice-ten [80] and ice-eleven where the hydrogen atoms are symmetrically placed) the hydrogen-bonding is disordered even down to 0 K, where reachable. Ice-four (IV) and ice-twelve (XII) [82] are both metastable within the ice-five phase space.
Cubic ice (Ic) is metastable with respect to hexagonal ice (Ih). It is worth emphasizing that liquid water is stable throughout its phase space above. Kurt Vonnegut's highly entertaining story concerning an (imaginary) ice-nine, which was capable of crystallizing all the water in the world [83], fortunately has no scientific basis (see also IE) as ice-nine, in reality, is a proton ordered form of ice-three, only exists at very low temperatures and high pressures and cannot exist alongside liquid water under any conditions. Ice Ih may be metastable with respect to empty clathrate structures of lower density under negative pressure conditions (i.e. stretched) at very low temperatures [520].
As pressure increases, the ice phases become denser. They achieve this by initially bending bonds, forming tighter ring or helical networks, and finally including greater amounts of network inter-penetration. This is particularly evident when comparing ice-five with the metastable ices (ice-four and ice-twelve) that may exist in its phase space.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||